"그래프"의 두 판 사이의 차이
DnlzkWiki
Administrator (토론 | 기여) (새 문서: 그래프란, 정점(vertex)과 간선(edge)의 집합이다. 이 글은 PS에 적합한 그래프에 대한 주제를 다룬다. 섬네일|그래프. 위 그래프는 6개의 정점(A~F)와 6개의 간선으로 이루어져 있다. ==용어 정의== * 정점(vertex, 때로는 노드(node) 라고도 한다) : 자료의 기본 단위. * 간선(edge) : 정점의 연결이다. 간선은 그 자체에 방향성이나 가중치 등이 존재할 수 있다....) |
Administrator (토론 | 기여) |
||
| 1번째 줄: | 1번째 줄: | ||
그래프란, 정점(vertex)과 간선(edge)의 집합이다. 이 글은 PS에 | 그래프란, 정점(vertex)과 간선(edge)의 집합이다. 이 글은 PS에 주로 출제되는 그래프에 대한 주제를 다룬다. | ||
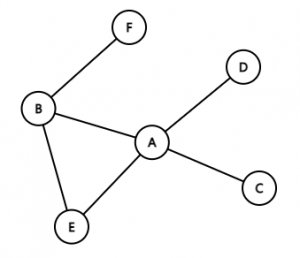
[[파일:Graph.png|섬네일|그래프. 위 그래프는 6개의 정점(A~F)와 6개의 간선으로 이루어져 있다.]] | [[파일:Graph.png|섬네일|그래프. 위 그래프는 6개의 정점(A~F)와 6개의 간선으로 이루어져 있다.]] | ||
| 5번째 줄: | 5번째 줄: | ||
* 정점(vertex, 때로는 노드(node) 라고도 한다) : 자료의 기본 단위. | * 정점(vertex, 때로는 노드(node) 라고도 한다) : 자료의 기본 단위. | ||
* 간선(edge) : 정점의 연결이다. 간선은 그 | * 간선(edge) : 정점의 연결이다. | ||
**간선은 방향성을 가질 수 있다. 방향성을 가진 그래프를 Directed 되었다고 한다. | |||
**간선은 가중치를 가질 수 있다. 가중치를 가진 그래프를 Weighted 되었다고 한다. | |||
*무향 그래프(undirected graph) : 간선에 방향이 없는 보통의 그래프이다. | |||
**인접성(adjacent) : 두 정점을 연결하는 간선이 존재한다면, 두 정점이 인접한다고 한다. | |||
**차수(degree) : 특정 정점을 연결하는 간선의 수 | |||
**연결성(connectivity) : 그래프의 어떤 두 정점을 잡아도, 그 두 정점을 양 끝점으로 하는 경로가 존재하는 성질을 의미한다. | |||
***연결되어 있지 않은 그래프는, 두 개 이상의 연결된 성분(component)으로 이루어져 있다. | |||
***성분은 연결되어 있어야 하며, 서로 다른 두 성분 사이에는 인접한 정점쌍이 존재하지 않아야 한다. | |||
**단절점(articulation point) : 그래프에서 한 정점과 그것과 연결된 간선을 제거했을 때, 그래프이 성분의 수가 증가하는 점을 단절점이라고 한다. | |||
**단절선(Bridges) : 그래프에서 한 간선을 제거했을 때, 그래프의 성분의 수가 증가하는 간선을 단절선이라고 한다. | |||
**이중 연결성(biconnectivity) : 그래프 G가 이중 연결되었다는 뜻은, G가 연결되어 있으면서, 단절점이 존재하지 않는 것을 의미한다. | |||
***이중 연결 요소(Biconnected Component) : 그래프 G'의 부분 그래프 G가 이중 연결 요소라는 뜻은, G가 maximal한 이중 연결 그래프임을 의미한다. | |||
*유향 그래프(방향 그래프, directed graph, digraph) : 간선에 '방향'이라는 속성을 추가한 그래프이다. | |||
**진입 차수(indegree) : 특정 정점으로 들어오는 간선의 수 | |||
**진출 차수(outdegree) : 특정 정점에서 나가는 간선의 수 | |||
**강연결성(Strongly connectivity) : 유향 그래프 G가 강연결 되었다는 뜻은, 그래프의 정점 G의 모든 정점 쌍 (u, v)에 대해, u에서 v로 가는 경로가 존재함을 의미한다. | |||
*특수 그래프 | |||
**완전 그래프(Complete graph) : 그래프의 모든 정점 쌍이 인접한 그래프이다. 정점이 n개인 완전 그래프를 보통 K_n으로 나타낸다. | |||
**이분 그래프(Bipartite graph) : 그래프의 정점의 부분집합 U와 그 여집합 V에 대해, U에 포함된 모든 정점의 쌍이 인접하지 않고, V에 포함된 모든 정점의 쌍이 인접하지 않는다고 하자. 이러한 정점의 부분집합 U가 존재할 때 그래프가 이분되었다고 하고, 그러한 그래프를 이분 그래프라고 한다. | |||
**완전 이분 그래프(Complete Bipartite graph) : 어떤 그래프가 이분 그래프이면서, | |||
== 그래프와 관련된 주제 == | |||
* 순회 : 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS) | |||
** DFS Tree / DFS Ordering : 그래프에 관련된 문제를 더 생각하기 쉽게 하는 트릭이다. | |||
* To be Continued.. | |||
2023년 8월 15일 (화) 13:44 기준 최신판
그래프란, 정점(vertex)과 간선(edge)의 집합이다. 이 글은 PS에 주로 출제되는 그래프에 대한 주제를 다룬다.
용어 정의
- 정점(vertex, 때로는 노드(node) 라고도 한다) : 자료의 기본 단위.
- 간선(edge) : 정점의 연결이다.
- 간선은 방향성을 가질 수 있다. 방향성을 가진 그래프를 Directed 되었다고 한다.
- 간선은 가중치를 가질 수 있다. 가중치를 가진 그래프를 Weighted 되었다고 한다.
- 무향 그래프(undirected graph) : 간선에 방향이 없는 보통의 그래프이다.
- 인접성(adjacent) : 두 정점을 연결하는 간선이 존재한다면, 두 정점이 인접한다고 한다.
- 차수(degree) : 특정 정점을 연결하는 간선의 수
- 연결성(connectivity) : 그래프의 어떤 두 정점을 잡아도, 그 두 정점을 양 끝점으로 하는 경로가 존재하는 성질을 의미한다.
- 연결되어 있지 않은 그래프는, 두 개 이상의 연결된 성분(component)으로 이루어져 있다.
- 성분은 연결되어 있어야 하며, 서로 다른 두 성분 사이에는 인접한 정점쌍이 존재하지 않아야 한다.
- 단절점(articulation point) : 그래프에서 한 정점과 그것과 연결된 간선을 제거했을 때, 그래프이 성분의 수가 증가하는 점을 단절점이라고 한다.
- 단절선(Bridges) : 그래프에서 한 간선을 제거했을 때, 그래프의 성분의 수가 증가하는 간선을 단절선이라고 한다.
- 이중 연결성(biconnectivity) : 그래프 G가 이중 연결되었다는 뜻은, G가 연결되어 있으면서, 단절점이 존재하지 않는 것을 의미한다.
- 이중 연결 요소(Biconnected Component) : 그래프 G'의 부분 그래프 G가 이중 연결 요소라는 뜻은, G가 maximal한 이중 연결 그래프임을 의미한다.
- 유향 그래프(방향 그래프, directed graph, digraph) : 간선에 '방향'이라는 속성을 추가한 그래프이다.
- 진입 차수(indegree) : 특정 정점으로 들어오는 간선의 수
- 진출 차수(outdegree) : 특정 정점에서 나가는 간선의 수
- 강연결성(Strongly connectivity) : 유향 그래프 G가 강연결 되었다는 뜻은, 그래프의 정점 G의 모든 정점 쌍 (u, v)에 대해, u에서 v로 가는 경로가 존재함을 의미한다.
- 특수 그래프
- 완전 그래프(Complete graph) : 그래프의 모든 정점 쌍이 인접한 그래프이다. 정점이 n개인 완전 그래프를 보통 K_n으로 나타낸다.
- 이분 그래프(Bipartite graph) : 그래프의 정점의 부분집합 U와 그 여집합 V에 대해, U에 포함된 모든 정점의 쌍이 인접하지 않고, V에 포함된 모든 정점의 쌍이 인접하지 않는다고 하자. 이러한 정점의 부분집합 U가 존재할 때 그래프가 이분되었다고 하고, 그러한 그래프를 이분 그래프라고 한다.
- 완전 이분 그래프(Complete Bipartite graph) : 어떤 그래프가 이분 그래프이면서,
그래프와 관련된 주제
- 순회 : 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)
- DFS Tree / DFS Ordering : 그래프에 관련된 문제를 더 생각하기 쉽게 하는 트릭이다.
- To be Continued..