Convex Hull

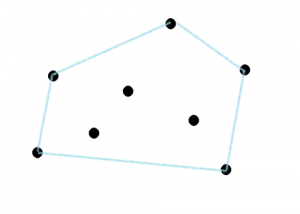
Convex Hull(볼록 껍질)은 주어진 모든 점을 포함하는 가장 작은 볼록다각형이다.

Graham Scan

https://www.crocus.co.kr/1288

1. 기준점을 잡는다. (보통 y좌표가 가장 작은 점을 기준으로 한다)
2. 기준점으로 하여 다른 점들을 반시계 방향으로 정렬한다.
3. 첫 번째와 두 번째 정점을 스택에 넣고 시작한다.
4. 스택에서 second와 first를 순서대로 꺼내고 next값과 ccw를 하여 > 0인지 확인한다. (좌회전 하는지 확인)
5. 좌회전한다면 볼록 껍질이 될 수 있다는 의미이고 pop했던 second를 다시 스택에 넣어 주고 next도 스택에 넣어 준다.
6. 우회전한다면 second 점은 버리고 first를 스택에 넣는다.
7. 4번 과정을 next값이 없을 때까지 반복한다.

스택에 남아 있는 점들이 Convex Hull이다.

MonotoneChain

1. Convex Hull을 상부와 하부로 나눈다.
2. 점들은 먼저 정렬한 이후 Graham Scan과정과 같이 ccw를 사용하여 스택에 넣어준다.
3. 하부는 상부 배열을 뒤집어 위 과정을 수행해준다.
4. 상,하부에 겹치는 점들이 있으므로 그들을 제외 시키고 스택을 합친다.

합쳐진 스택이 ConvexHull이다. <syntaxhighlight lang="python" line="1"> import sys input=sys.stdin.readline def ccw(p1,p2,p3):

   return p1[0]*(p2[1] - p3[1]) + p2[0]*(p3[1] - p1[1]) + p3[0]*(p1[1] - p2[1])

def monotone(points):

   points.sort()
   lower=[]
   upper=[]
   for i in points:
       while len(lower) > 1 and ccw(lower[-2],lower[-1],i) < 0:
           lower.pop()
       lower.append(i)
   for j in reversed(points):
       while len(upper) > 1 and ccw(upper[-2],upper[-1],j) < 0:
           upper.pop()
       upper.append(j)
   return lower[:-1]+upper[:-1]

dots=[] n=int(input()) for k in range(n):

   x,y,c = input().split()
   if c == 'Y':
       dots.append([int(x),int(y)])

dots=monotone(dots) print(len(dots)) for l in dots:

   print(l[0],l[1])